Sensor Fusion
What is Sensor Fusion
Sensor fusion is combining of sensory data or data derived from disparate sources such that the resulting information has less uncertainty than would be possible when these sources were used individually. The term uncertainty reduction in this case can mean more accurate, more complete, or more dependable, or refer to the result of an emerging view, such as stereoscopic vision (calculation of depth information by combining two-dimensional images from two cameras at slightly different viewpoints).
The data sources for a fusion process are not specified to originate from identical sensors. One can distinguish direct fusion, indirect fusion and fusion of the outputs of the former two. Direct fusion is the fusion of sensor data from a set of heterogeneous or homogeneous sensors, soft sensors, and history values of sensor data, while indirect fusion uses information sources like a priori knowledge about the environment and human input
How Sensor Fusion works
Sensor fusion is the art of combining multiple physical sensors to produce accurate "ground truth", even though each sensor might be unreliable on its own.
How do you know where you are? What is real? That’s the core question sensor fusion is supposed to answer. Not in a philosophical way, but the literal “Am I about to autonomously crash into the White House? Because I’ve been told not to do that” way that is built into the firmware of commercial Quadcopters.
Sensors are far from perfect devices. Each has conditions that will send them crazy.
Inertial Measurement Units are a classic case—there are IMU chips that seem superior on paper, but have gained a reputation for “locking up” in the field when subjected to certain conditions, like flying 60kph through the air on a quad-copter without rubber cushions.
In these cases the IMU can be subject to vibrations—while inside spec—that can match harmonics with micro-mechanical parts. The IMU may have been designed for use in a mobile phone with a wobbler, not next to multiple motors humming at 20,000 RPM. Suddenly the robot thinks it’s flipping upside down (when it’s not) and rotates to compensate. Some pilots fly with data-loggers, and have captured the moment when the IMU bursts with noise immediately before a spectacular crash.
So, how do we cope with imperfect sensors? We can add more, but aren't we just compounding the problem?
Your blind spots get smaller the more sensors you have. But the math gets harder in order to deal with the resulting fuzziness. Modern algorithms for doing sensor fusion are “Belief Propagation” systems—the Kalman filter being the classic example.
Types of Sensor Fusion algorithm
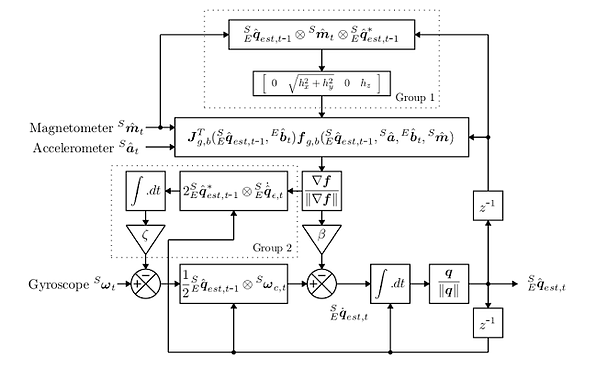
There are a variety of sensor fusion algorithms out there, but the two most common in small embedded systems are the Mahony and Madgwick filters. Mahony is more appropriate for very small processors, whereas Madgwick can be more accurate with 9DOF systems at the cost of requiring extra processing power (it isn't appropriate for 6DOF systems where no magnetometer is present, for example).
For details of Madgwick, you need to check the link.
Madwick algorithm block diagram
The Kalman Filter
At its heart, the algorithm has a set of “belief” factors for each sensor. Each loop, data coming from the sensors is used to statistically improve the location guess, but the quality of the sensors is judged as well.
Robotic systems also include constraints that encode the real-world knowledge that physical objects move smoothly and continuously through space (often on wheels), rather than teleporting around like GPS coordinate samples might imply.
That means if one sensor which has always given excellent, consistent values starts telling you unlikely and frankly impossible things (such as GPS/radio systems when you go into a tunnel), that sensors' believability rating gets downgraded within a few millisecond iterations until it starts talking sense again.
This is better than just averaging or voting because the Kalman filter can cope with the majority of its sensors going temporarily crazy, so long as one keeps making good sense. It becomes the lifeline that gets the robot through the dark times.
The Kalman filter is an application of the more general concepts of Markov Chains and Bayesian Inference, which are mathematical systems that iteratively refine their guesses using evidence. These are tools designed to help science itself test ideas (and are the basis of what we call “statistical significance”).

It could, therefore, be poetically said that some sensor fusion systems are expressing the very essence of science, a thousand times per second.
Kalman filters have been used for orbital station-keeping on space satellites for decades, and they are becoming popular in robotics because modern microcontrollers are capable enough to run the algorithm in real time. An Interactive Tutorial for Non-Experts
PID Filters
Simpler robotic systems feature PID filters. These can be thought of as primitive Kalman filters fed by one sensor, with all the iterative tuning hacked off and replaced with three fixed values.
Even when PID values are auto tuned or set manually, the entire “tuning” process (adjust, fly, judge, repeat) is an externalized version of Kalman with a human doing the belief-propagation step. The basic principles are still there.
Some other Filter
Real systems are often hybrids, somewhere between the two.
The full Kalman includes “control command” terms that make sense for robots, as in: “I know I turned the steering wheel left. The compass says I’m going left, the GPS thinks I’m still going straight. Who do I believe?”
Even for a thermostat—the classic simplest control-loop—a Kalman filter understands that it can judge the quality of thermometers and heaters by fiddling with the knob and waiting to see what happens. Individual sensors usually can’t affect the real world, so those terms drop out of the math and much power goes with them. But you can still apply the cross-checking belief propagation ideas and “no teleporting” constraints, even if we can’t fully close the control loop.